The world's first demonstration of the high-efficiency hydrogen liquefaction by magnetic refrigeration
In hydrogen liquefaction by the magnetic refrigeration, the adiabatic
demagnetization method to generate temperature below 1 K is extended to
the high-temperature region.
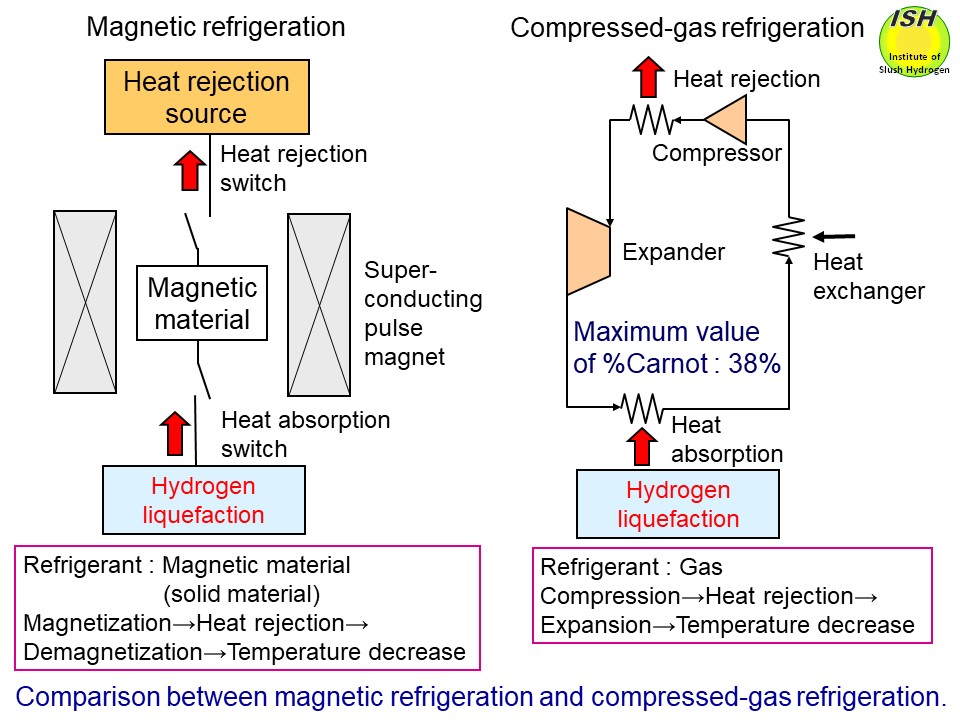
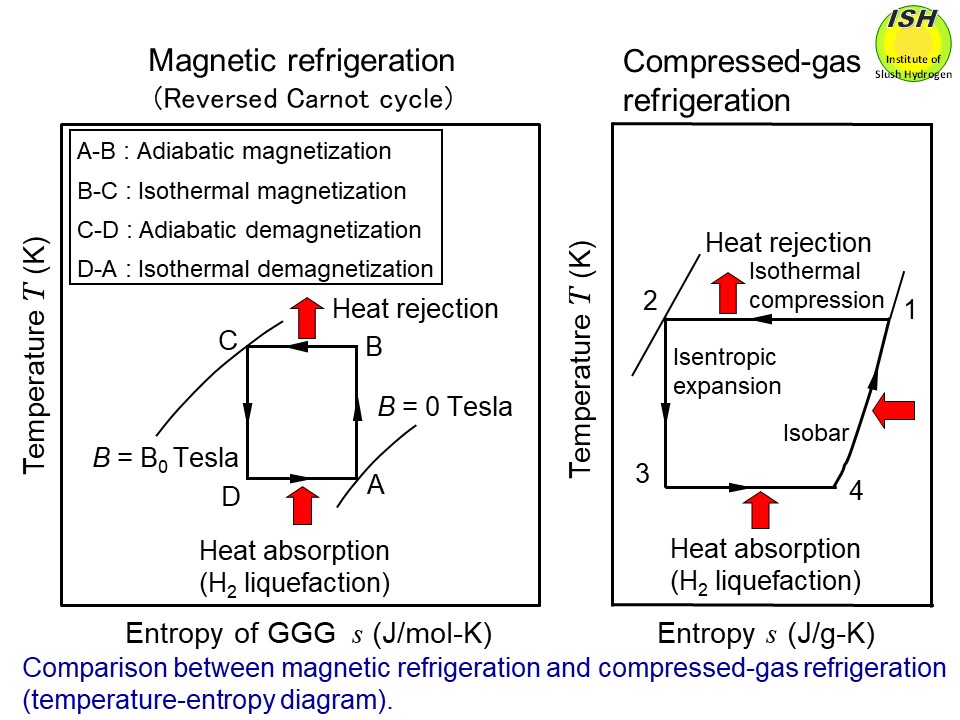
The principles of the magnetic refrigeration and the compressed-gas refrigeration
are illustrated in the above figure. The temperature-entropy diagrams of magnetic material and gas as a refrigerant
in liquefaction cycle are respectively presented in the above figure. The magnetic refrigeration for hydrogen liquefaction uses an external
magnetic field to magnetize and demagnetize a magnetic material in repeated
cycles, thus producing low temperatures through the magnetocaloric effect.
Since the magnetic refrigeration method can ideally realize the reversed
Carnot cycle, it is possible to achieve theoretically a higher %Carnot
efficiency* in contrast to the compressed-gas refrigeration method as noted
in the above figures [4].
The maximum efficiency is expected to be about 50% in terms of the %Carnot
efficiency*, compared to about 38% of the %Carnot efficiency for the world’s
largest hydrogen liquefier (liquefaction capacity: 60 ton/day) using the
compressed-gas method. Also, given the use of solid magnetic material,
which has much greater entropy density than gas, the liquefier can be made
compact.
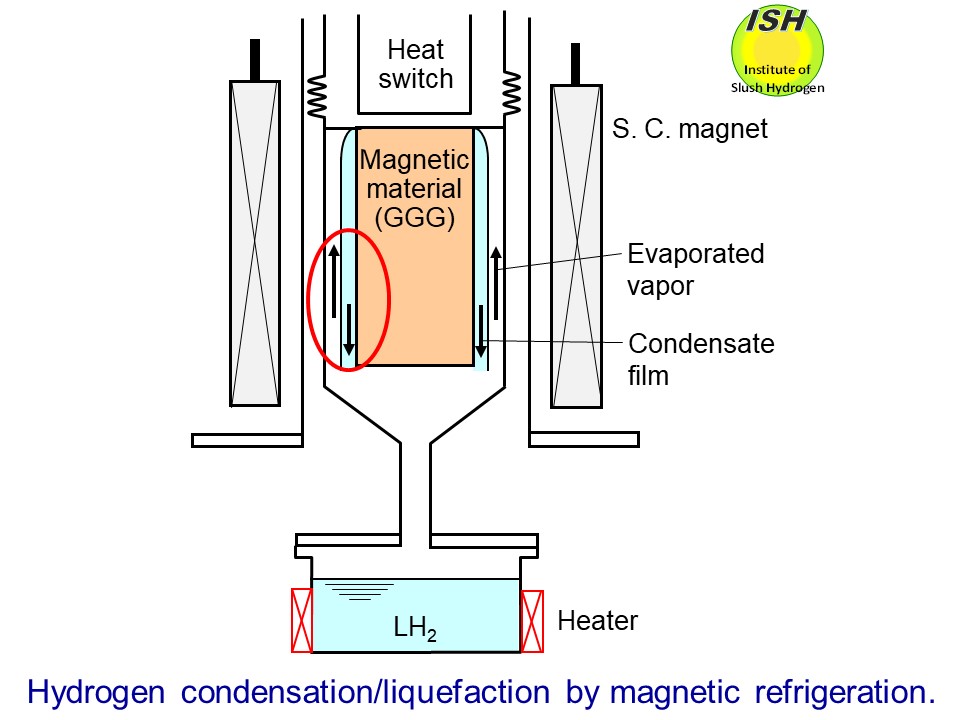
In the experiment, hydrogen gas evaporated in a liquid hydrogen vessel,
as shown in the figure below, was liquefied by using magnetic refrigeration. Gadolinium gallium garnet
(GGG: Gd3Ga5O12) was selected as a magnetic material. The magnetic refrigerator maimly
consists of a superconducting pulse magnet (the maximum field of 5 Tesla
and the maximum magnetization/demagnetization sweep rate of 0.36 T/s),
a Gifford-McMahon type refrigerator (UCR31W made by MHI) as a heat rejection
source (Th = 25 K), and a heat pipe as a heat absorption switch for hydrogen liquefaction
(Tl = 20.3 K) [8, 9]. In the thermal design of the high-performance heat pipe,
the Nusselt eq. was applied to evaluate the condensing heat-transfer coefficient
of hydrogen as described in "Hydrogen condensation and liquefaction".
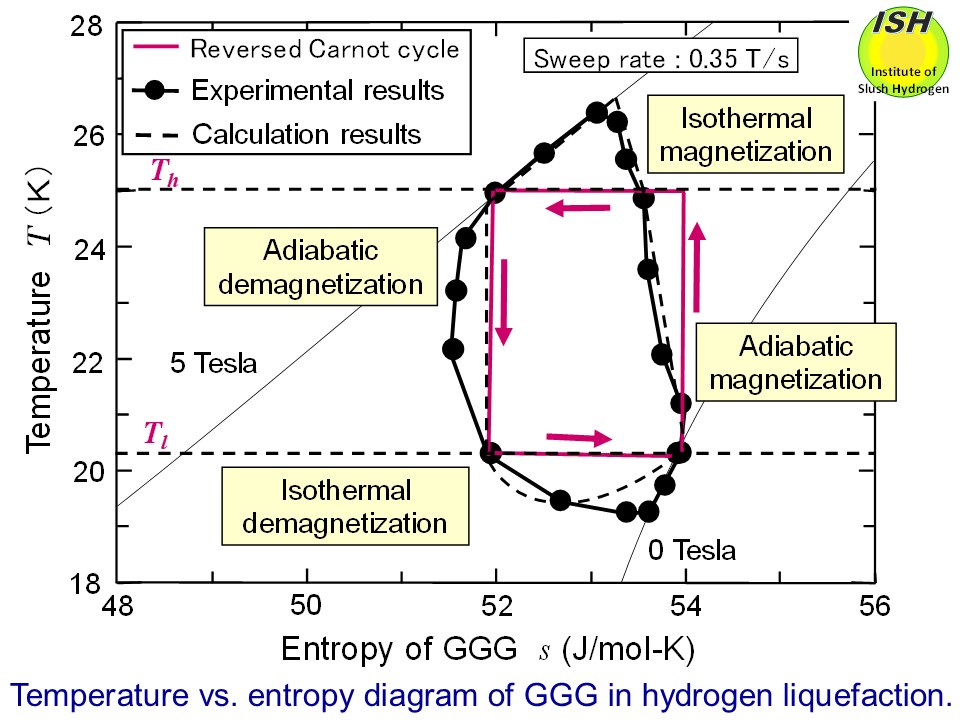
The temperature-entropy diagram of magnetic material (GGG) obtained in
the hydrogen liquefaction experiment at 0.35 T/s, the reversed Carnot cycle,
and the calculation results using a simulation model are illustrated in
the figure below. The reasons the ideal reversed Carnot cycle indicated as a rectangle
cannot be realized are the insufficient heat-transfer performance of the
heat absorption and heat rejection switches, and the influence of uncondensed
hydrogen gas (continuously evaporating in the liquid hydrogen vessel) around
the magnetic material.
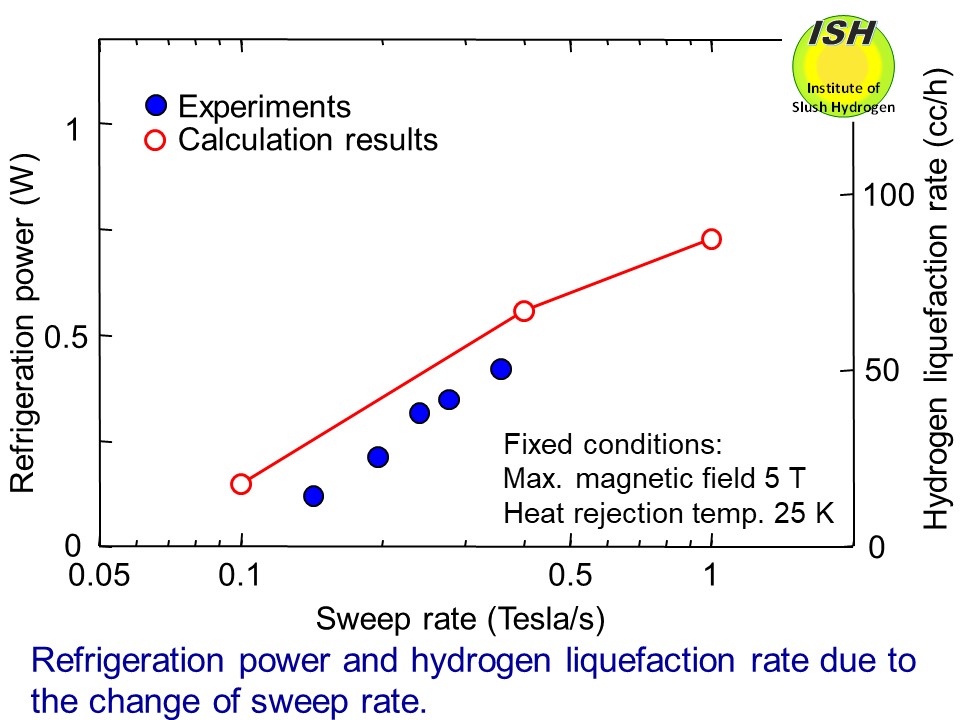
In the hydrogen liquefaction experiment at the fastest magnetization/demagnetization
rate of 0.36 T/s, as shown in the figure below, the maximumrefrigeration power (at 20.3 K) of 0.4 W (liquefaction rate: 3.55 g/h or 50 cc/h) with the %Carnot
efficiency* of 37% and the liquefaction efficiency** of 78% was obtained.
The achievement of 37% for the %Carnot efficiency in a small-scale liquefaction
experiment (3.55 g/h or 50 cc/h) demonstrates the high efficiency of this
method.
The world’s first high-efficiency hydrogen liquefaction by the magnetic
refrigeration is also demonstrated [8, 9].
The details of the study and experimental results are given on "Web site" below.
For hydrogen liquefaction, a multistage magnetic refrigerator from room
temperature to liquid hydrogen temperature has been proposed, and research
and development work is in progress.A method has also been proposed for producing slush hydrogen from liquid
hydrogen, using magnetic refrigeration to produce temperature below 14
K.
* %Carnot efficiency: The ratio of the reversed Carnot work to the actual
work per unit mass liquefied. %Carnot efficiency = FOM (Figure of Merit)×100
(%).
** Liquefaction efficiency: The ratio of the rerigeration power of the
experiment to that of the reversed Carnot cycle at the refrigeration (or
liquefaction) temperature.
Details of our hydrogen liquefaction study by magnetic refrigeration are
shown here.
Temperature-entropy diagram of GGG, refrigeration power and hydrogen liquefaction rate