Nucleate pool boiling heat transfer to slush hydrogen and slush nitrogen

　When stored liquid or slush hydrogen is used as the refrigerant for the high-temperature SMES, it is important to consider nuclear pool boiling heat transfer properties.

　We used a 0.025 m diameter circular flat-plate made of copper as a heat transfer surface. The heat transfer surface was placed in differing orientations (horizontal upward facing, vertical, and horizontal downward facing) to investigate nuclear pool boiling heat transfer to liquid hydrogen at the normal boiling point (0.1 MPa, 20 K: NBP liquid), liquid hydrogen at the triple point pressure (0.007 MPa, 14 K: TP liquid), and settled slush hydrogen at the triple-point pressure (0.007 MPa, 14 K: TP slush). In the experiments, mass solid fractions of 20-35 wt.% were used, and the critical heat flux (CHF) was verified. Heat transfer was also similarly measured for liquid and slush nitrogen [25].

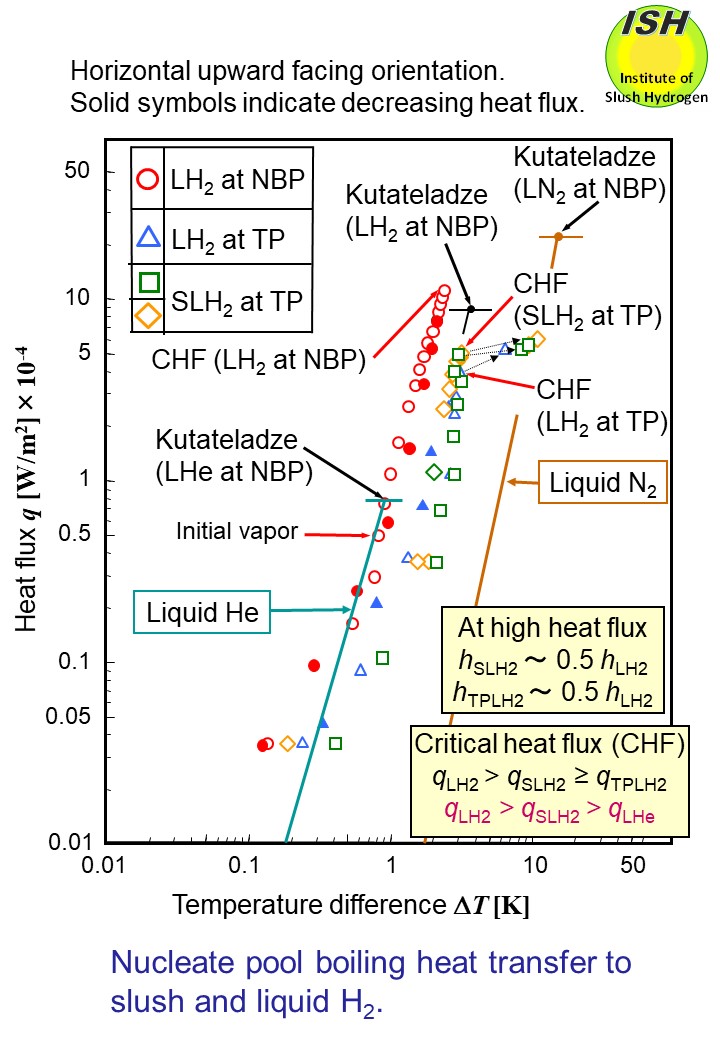
　The above figure illustrates heat transfer to NBP liquid hydrogen, TP liquid hydrogen and TP slush hydrogen in the case of the horizontal upward facing orientation. Heat flux q is indicated on the vertical axis, while the temperature difference ∆T (superheat) is indicated on the horizontal axis. Also, using the Kutateladze eq. applied to the horizontal upward facing orientation, calculated CHF values q* for liquid hydrogen, liquid nitrogen, and liquid helium are given.

　For NBP liquid, the heat transfer coefficient h (h = q /∆T) was about that of liquid helium, while the heat transfer coefficient for TP slush in the high heat flux region fell to approximately 0.5 times that of NBP liquid.

　When comparing CHF values q* = 11 W/cm² (ΔT = 2 K) for NBP liquid with q* = 5 W/cm² (ΔT = 2.5 K) for TP slush hydrogen and q* = 0.8 W/cm² (ΔT = 0.8 K) for liquid helium in the case of a horizontal upward facing orientation, NBP liquid hydrogen is characterized by the greatest heat transfer coefficient and the highest CHF.

　For transport via pipeline to a remote location, because heat inleak during such transport would melt the solid hydrogen particles, it is predicted that storage would be in the form of liquid hydrogen. In this case, the use of liquid hydrogen as the refrigerant in a SMES system would be advantageous from the standpoint of heat transfer properties.

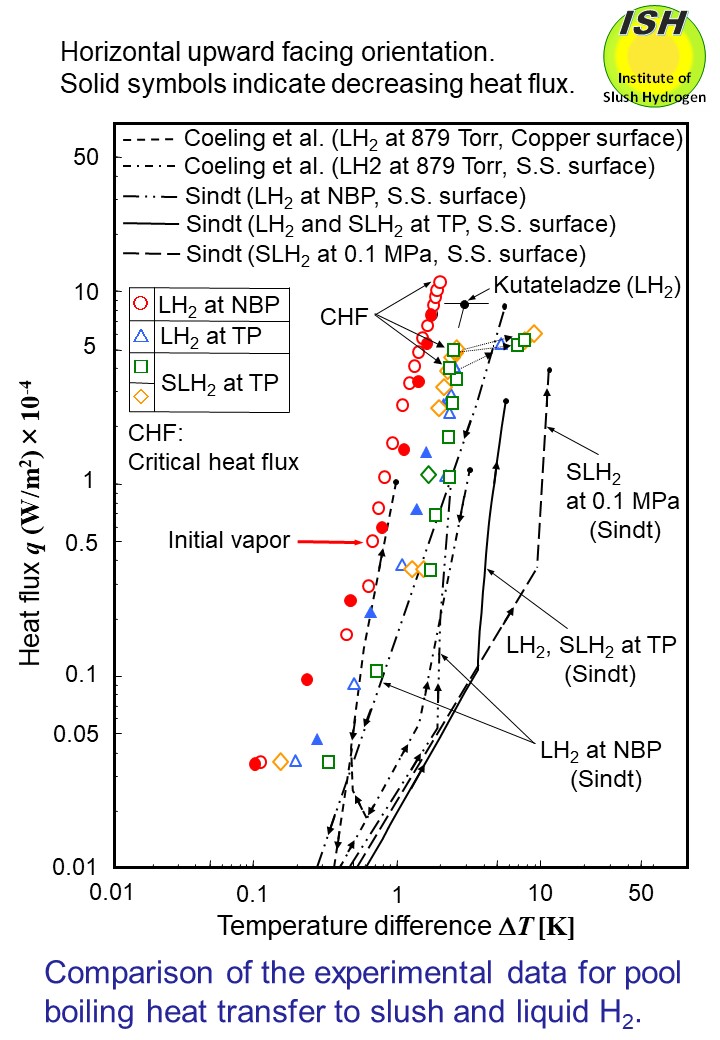
　The figure below shows the results of Coeling et al. [55] obtained from the circular flat plate heat transfer surface (roughness of the heat transfer surface: 0.13 μm) 0.0254 m in diameter in liquid hydrogen for comparison between copper and stainless steel used for the heat transfer surface. The figure also shows the results of Sindt [56] using the circular heat transfer surface made of stainless steel 0.0254 m in diameter (roughness of the heat transfer surface unknown) with mass solid fractions of 45 wt.%, and the present results obtained from the circular flat plate heat transfer surface made of copper (roughness of the heat transfer surface: 0.2 μm) 0.025 m in diameter. In Sindt’s experiment, the heat transfer data was obtained in a region of relatively small heat fluxes from the natural convection region to the nucleate boiling region in the respective cases of the heat transfer surface; horizontal surface facing up, vertical surface and horizontal surface facing down, and the heat transfer characteristics from the large heat flux region to the critical heat flux (CHF), practically important, were not confirmed.
　The results obtained from the present experiments in the nucleate boiling region of liquid hydrogen at NBP tend to show those similar to the results of Coeling et al. for the copper heat transfer surface and show a trend similar to Sindt’s boiling curve. Deviation of the present results to the left from Sindt’s curve may probably be due to the differences in the material for the heat transfer surface and the surface roughness.
　In Sindt’s experiment, if the orientation of the heat transfer surface in the nucleate boiling region remains the same, the value of heat flux q corresponding to the same value of ΔT becomes the largest with liquid hydrogen, showing equal values of heat flux for liquid hydrogen at TP and slush hydrogen. In the present experiments on the other hand, the value of heat flux q to the same value of ΔT becomes smaller in an order of liquid hydrogen at NBP, liquid hydrogen at TP and slush hydrogen. Although the difference in heat flux value between liquid hydrogen at TP and slush hydrogen is small, this difference is clearly recognized (refer to the figures below described later: heat flux q vs. heat transfer coefficient h of H₂ and N₂).

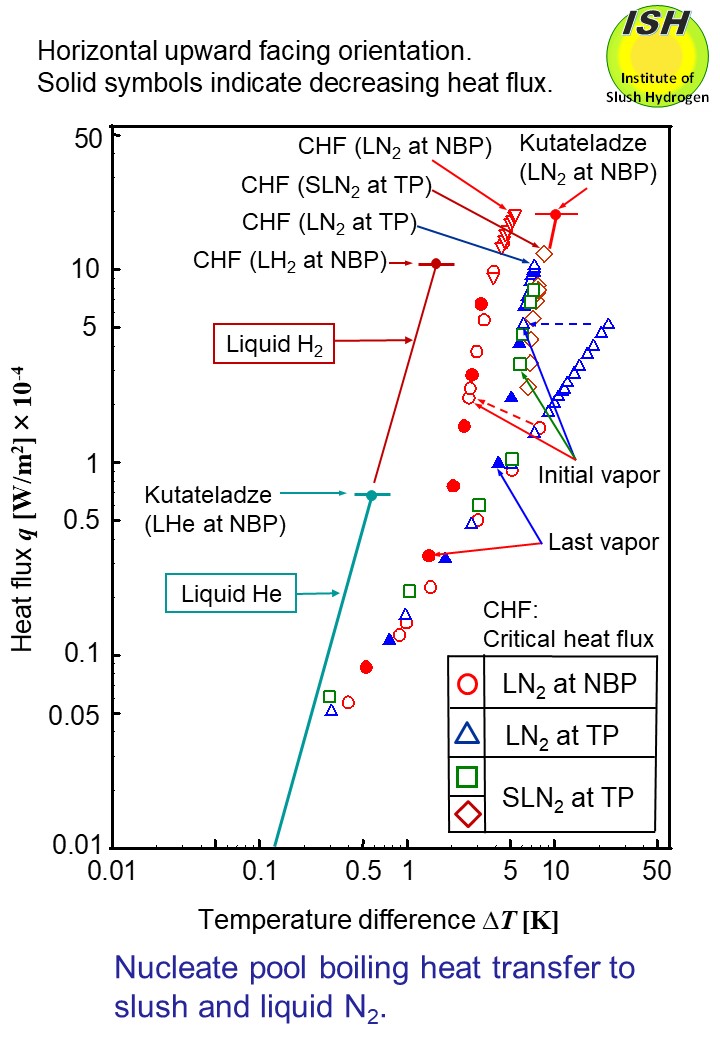
　It is also noteworthy that, as shown in the figure below for liquid nitrogen, CHF q* = 20 W/cm² (ΔT = 6 K) is about twice as large as for liquid hydrogen, while at the same heat flux, the heat transfer coefficient falls to a level of 0.4 times.

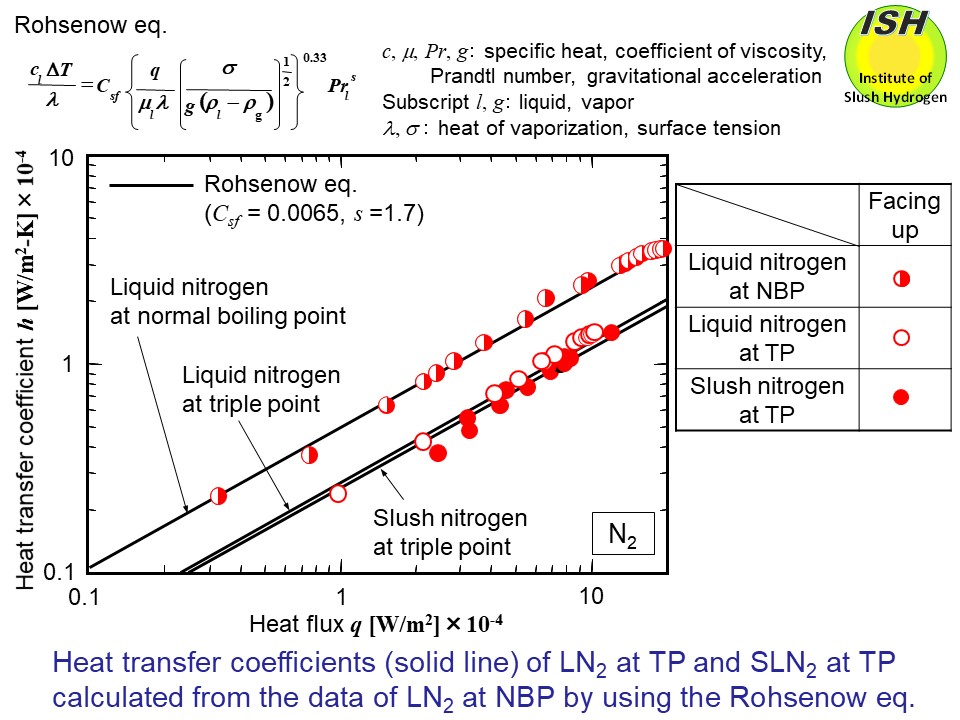
　The figure below illustrates heat transfer to NBP liquid nitrogen, TP liquid nitrogen and TP slush nitrogen in the case of the horizontal upward facing orientation.

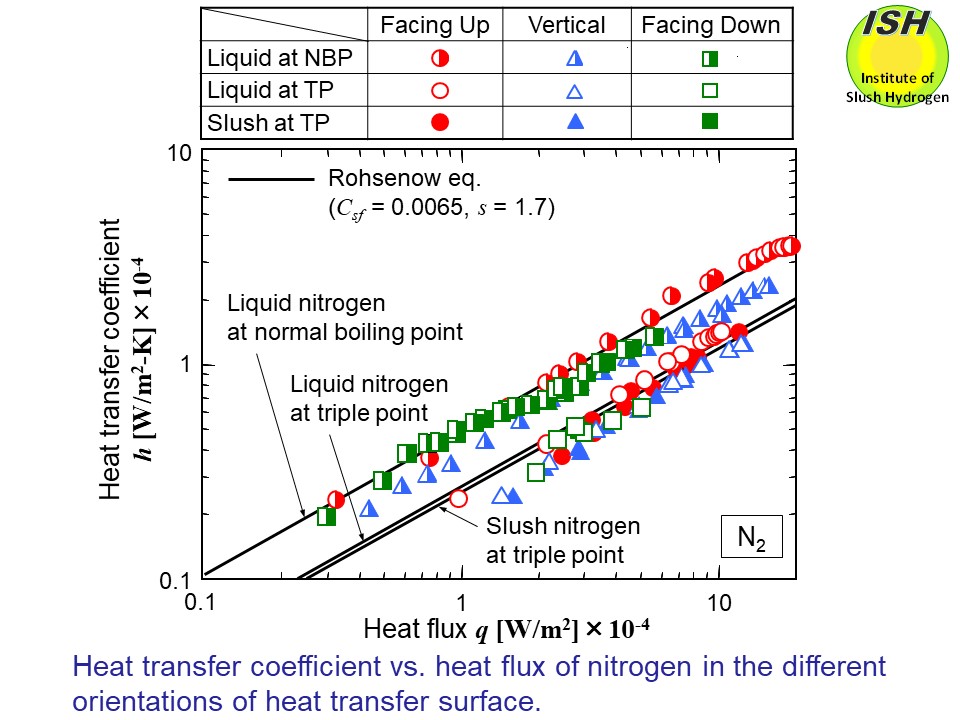
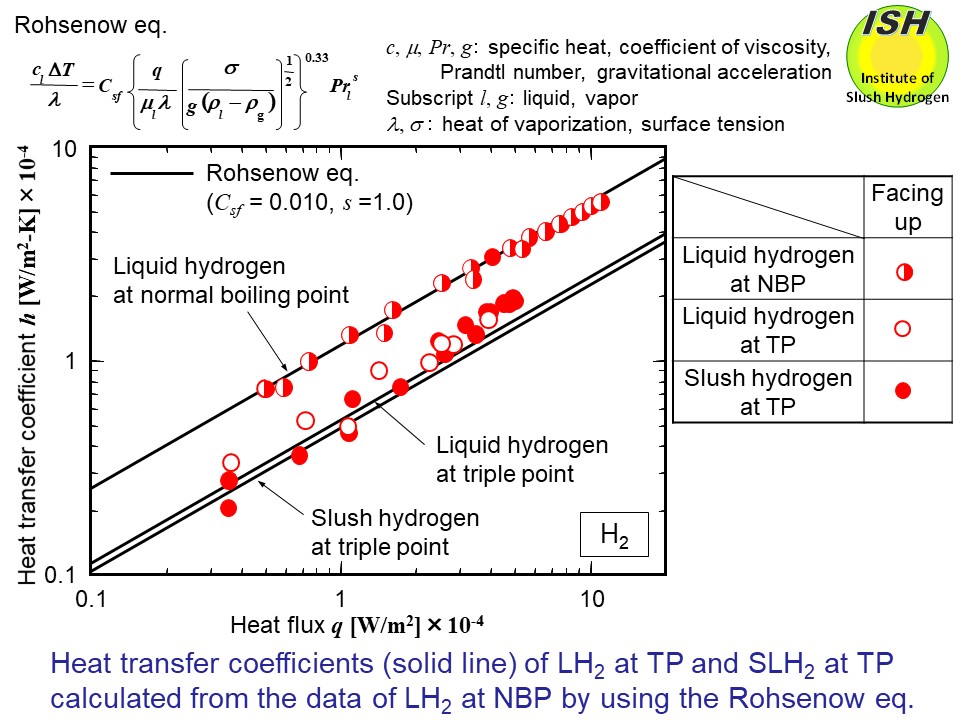
　The figures below present heat transfer to NBP liquid, TP liquid and TP slush of hydrogen and nitrogen in the case of different orientations (horizontal upward facing, vertical and horizontal downward facing), respectively. The solid lines in the figure show the calculated results of TP liquid and TP slush from the experimental data of NBP liquid using the Rohsenow eq. as described below.

　The experimental results for the TP slush hydrogen and nitrogen were compared with the Rohsenow eq. (refer to the figure below) [31], and consideration was given as to applicability with respect to a solid-liquid two-phase fluid. The coefficients C_sf and s are values determined by the combination of the heat transfer surface material and the liquid, with the same value being applicable regardless of differences in the pressure of liquid. The thermo-physical values of the fluid were used with respect to the NBP and the TP states.
　First, after determining C_sf and s so as to satisfactorily express the actual experimental results for the NBP liquid (C_sf = 0.010, s = 1.0 for hydrogen and C_sf = 0.0065, s = 1.7 for nitrogen), the heat transfer coefficients for the TP liquid and the TP slush were predicted. Given the difficulty involved in the experimental work, it is important from a practical standpoint to be able to predict the heat transfer coefficient for solid-liquid two-phase slush using the experimental results for the NBP liquid. In the case of slush, the value used for the heat of vaporization λ includes the heat of fusion for the solid. The figures below present the calculation results for the TP liquid and the TP slush by the solid line in the case of the horizontal upward facing orientation because the Rohsenow eq. is proposed for the horizontal upward facing orientation.
　As a result of predicting the heat transfer coefficient for the TP slush hydrogen and nitrogen using experimental results of the NBP liquid hydrogen and nitrogen, and the Rohsenow eq., somewhat lower values of heat transfer coefficient for the TP slush hydrogen were obtained than those of the experimental results. However, these values were found to have a satisfactory fit to the experimental data.

　Comparing the CHF values for the NBP liquid hydrogen and the TP slush hydrogen with that of the NBP liquid helium, it can be seen that the former values are quite high, meaning thatliquid or slush hydrogen can be reasonably expected to be used as the refrigerant for superconducting machines using high-temperature superconducting material (MgB₂).

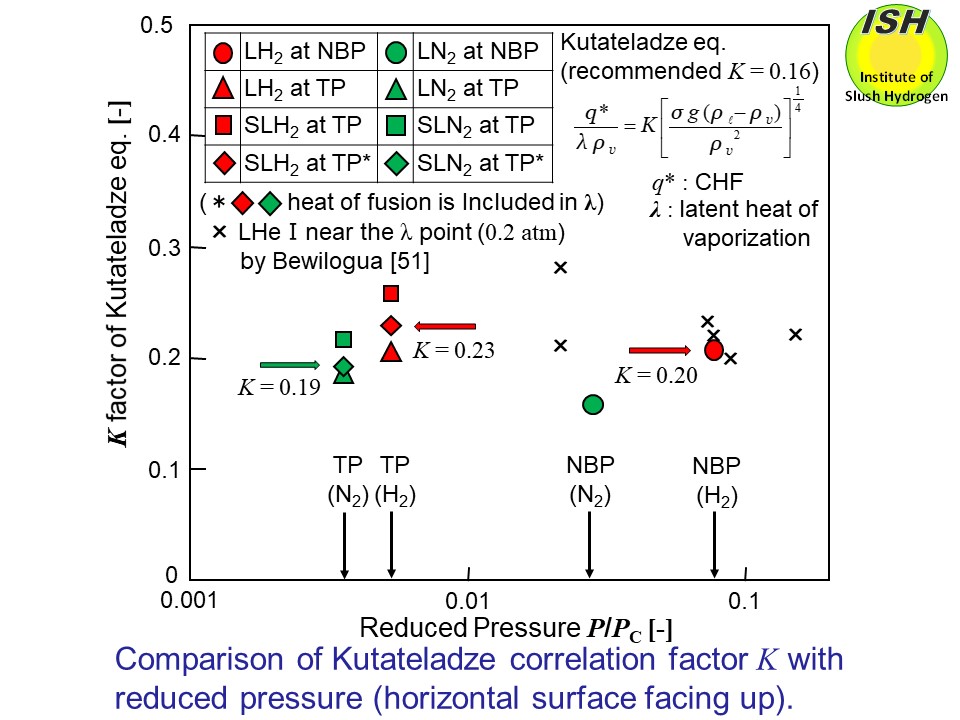
　Kutateladze gives the equation for the critical heat fluxq* in the nucleate pool boiling heat transfer to the horizontal heat transfer surface facing up as shown inthe figure below[31]. Although the factorKdiffers (0.095 ≦K≦ 0.20), depending on conditions of heat transfer, etc.,K＝0.16 proposed by Kutatelazde is generally recommended as a mean value in a good agreement to the experimental value.
　Calculations of the factor K in Kutateladze eq. from the critical heat flux values of horizontal surface facing up for the liquid at NBP, the liquid at TP and slush at TP are shown in the figure below. The ratios (P/P_c) of pressures to critical pressures in the respective fluids are shown along the axis of abscissas in the figure. The calculations for slush including the heat of fusion of the solid in the latent heat of vaporization are also shown. The figure also shows the experimental results of Bewilogua et al. [51, 52] at near the λ point (P／P_c＝0.02) of liquid helium. There have been no measurements in the region of P／P_c ＜ 0.02, and in the present experiment, the K value tends to increase in an order of the liquid at TP and the slush at TP over the liquid at NBP in both cases of hydrogen and nitrogen, and for the slush, approximately K ＝0.23 (H₂), 0.19 (N₂). (when the heat of fusion of the solid is included in the latent heat of vaporization).

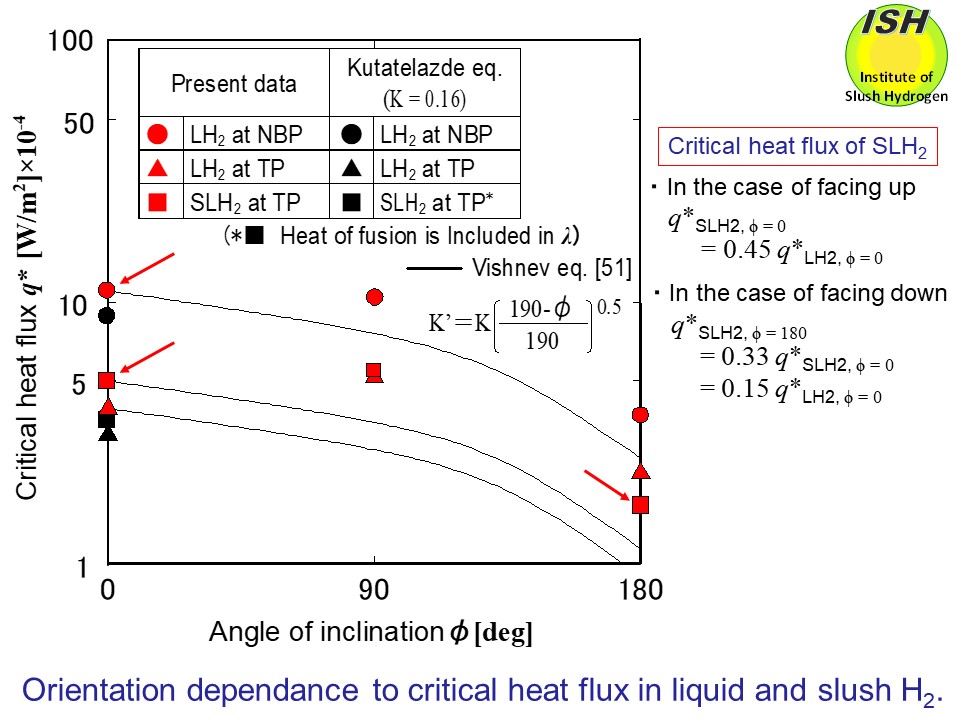
　Changes of the critical heat flux q* according to the inclination of the heat transfer surface are shown in the figure below. For reference, the figure also show the calculated results of the critical heat flux q* for the horizontal surface facing up using the factor K = 0.16 in the Kutateladze eq. For the slush, the calculations include the heat of fusion of the solid in the latent heat of vaporization λ. The figure also show the correlation of Vishnev (51) based on the horizontal surface facing up. The correlation of Vishnev uses K’＝K (190－Φ) ^0.5/190^0.5 instead of the factor K of Kutateladze eq.
　Lyon [53] conducted his experiment in liquid helium from the critical point to the λ point and showed that the critical heat flux decreases with an increase of the angle (Φ) of inclination of the heat transfer surface. There have been no published data on experiments systematically covering changes of the critical heat fluxes at near the triple-point pressure according to the inclination of the heat transfer surface for liquid hydrogen and liquid nitrogen, but the experiments of Class et al. [54] using angles of inclination Φ＝0°, 45° and 90° in liquid hydrogen at 0.82 atm show that there is hardly difference in the critical heat flux. The present experiments show that the liquid at TP and slush at TP exhibit slightly higher values in the orientation of vertical than in that of horizontal surface facing up. Also, the comparison with the correlation of Vishnev shows that the experimental results for both orientations of vertical surface and horizontal surface facing down are higher than the calculations. The critical heat flux values of slush hydrogen and slush nitrogen in the case of the heat transfer surface in its orientation of horizontal surface facing up decreased to 0.45 times and 0.62 times those of the liquid at NBP. In the case of horizontal surface facing down, the respective values decreased to 0.33 times and 0.43 times the critical heat flux values of slush in the case of horizontal surface facing up.